ECC – Khudri.com

Tahun 1985, Koblitz dan Miller mengenalkan kriptografi kurva elliptic (elliptic curve cryptography) yang menggunakan masalah logaritma diskrit pada titik kurva elliptic. Kriptografi kurva elliptic dapat digunakan untuk beberapa keperluan seperti skema enkripsi (contohnya ElGamal ECC), tanda tangan digital (contohnya ECDSA) dan protokol pertukaran kunci (contohnya Diffie-Hielman ECC).

Stallings [13] mendefinisikan kurva elliptic sebagai suatu kurva yang dibentuk oleh persamaan kubik dan memiliki persamaan umum
$\large y^{2}+Axy\: =\: x^{3}+Cx^{2}+Dx+E\; \; \; (4.1)$
$\large y^{2}+Axy\: =\: x^{3}+Cx^{2}+Dx+E\; \; \; (4.1)$

dengan A,B,C,D dan E adalah konstanta bilangan real. Domain x dan y adalah bilangan real ( $\large \mathbb{R}$ ). Dalam penulisan ini, tidak dibahas mengenai persamaan (4.1). Untuk mendukung tujuan penulisan ini, penulis akan menjelaskan bentuk kurva yang lebih sederhana dari persamaan (4.1), yaitu

$\large y^{2}\: =\: x^{3}+Ax+B\; \; \; (4.2)$

dengan A dan B dalam $\large \mathbb{R}$ serta x, y $\large \in$ $\large \mathbb{R}$ .

Gambar 4.1 merupakan salah satu contoh bentuk geometri dari kurva elliptic dengan persamaan $\large y^{2}\: =\: x^{3}+x+1$ . Setiap kurva elliptic akan berbentuk simetris terhadap sumbu x atau garis y=0. Karena untuk setiap nilai x $\large \in$ $\large \mathbb{R}$ , terdapat sepasang nilai y $\large \in$ $\large \mathbb{R}$ yang memenuhi persamaan (4.2), yaitu

$\large y_{1}=+\sqrt{x^{3}+Ax+B}$ dan $\large y_{2}=-\sqrt{x^{3}+Ax+B}$ .

Kurva elliptic juga dapat dipandang sebagai suatu himpunan yang terdiri dari titik-titik (x,y) yang memenuhi persamaan (4.2). Himpunan tersebut dinotasikan dengan E(A,B). Untuk setiap nilai A dan B yang berbeda, dihasilkan himpunan E(A,B) yang berbeda pula. Sebagai contoh, kurva dalam Gambar 4.1 dan Gambar 4.2.

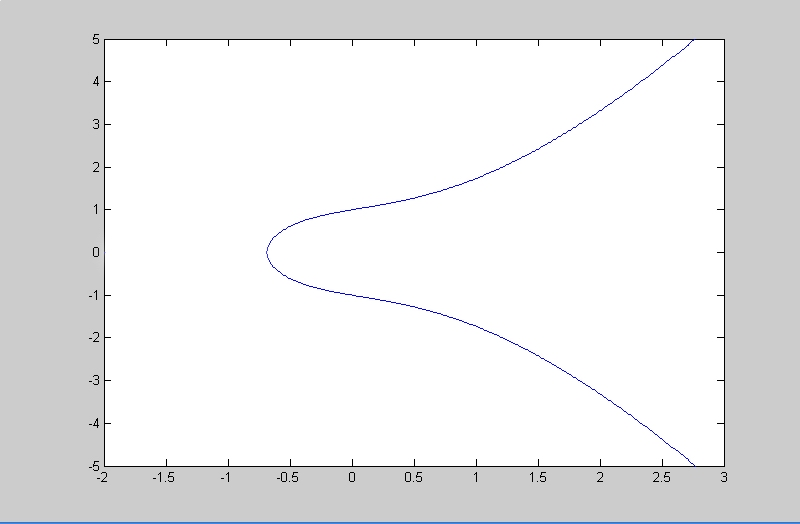
gbr-4-1
Gambar 4.1. Kurva Elliptic $\large y^{2}\: =\: x^{3}+x+1$

gbr-4-2
Gambar 4.2. Kurva Elliptic $\large y^{2}\: =\: x^{3}-x$

Source:
wan.khudri.com

Tag: ECC

Kriptografi Kurva Elliptic