Featured

Welcome

“Belajar dan Berbagi Ilmu” itulah yang menginspirasi saya untuk lebih mempermudah orang lain untuk saling berbagi dan belajar bersama. Meski karya ini sederhana, semoga bisa membantu siapapun yang membutuhkan referensi untuk “Belajar dan Berbagi Ilmu” khususnya yang berkaitan dengan Matematika, Keamanan Informasi (Information Security) yang berkaitan dengan Kriptografi (cryptography), terutama Kriptografi atau Kriptosistem Kurva Elliptic (Elliptic Curve Cryptosystems), salah satunya adalah ElGamal Elliptic Curve Cryptography.

All about: Matematika (Mathemathics), Kriptografi (Cryptography), Kurva Elliptic (Ellptic Curve), ElGamal, Kriptosistem Kurva Elliptik (Elliptic Curve Cryptosystems), ElGamal Elliptic Curve Cryptography, Field, Finite Field serta topik lain yang relevan dengan Kriptografi dan Matematika.

Cara Mengatasi Http Error di WordPress

Cara Mengatasi Http Error di WordPress – Upload Gambar di WordPress muncul Http Error – Fix Http Error WordPress.

Solusi Pertama:
Tambahkan kode berikut dalam file “.htaccess”.
SetEnv MAGICK_THREAD_LIMIT 1

Solusi Kedua:
Jika cara pertama gagal, solusi kedua adalah menambahkan kode berikut ke dalam file “functions.php” yang ada di theme wordpress (biasanya berada dalam direktori “wp-contents/themes/namatheme/”.
add_filter( ‘wp_image_editors’, ‘change_graphic_lib’ );
function change_graphic_lib($array) {
return array( ‘WP_Image_Editor_GD’, ‘WP_Image_Editor_Imagick’ );
}

Solusi Ketiga:
Jika cara pertama dan kedua gagal, Anda dapat mencoba cara ketiga,yaitu dengan menambahkan kode berikut ke dalam file “wp-config.php”.
define(‘WP_MEMORY_LIMIT’, ’64MB’);

Solusi Keempat:
Jika cara pertama sampai ketiga masih gagal, Login control panel hosting (cPanel atau yg lain), cek folder “uploads” (/wp-content/uploads/) dan pastikan “permission” folder “uploads” adalah 775.

Solusi Kelima:
Jika cara pertama sampai keempat masih gagal, cek plugins yang terinstal, apakah menggunakan plugins Image Optimizer?? Jika iya, non aktifkan terlebih dahulu dan lihat apakah dapat mengatasi error tersebut.

Solusi Keenam:
Jika cara pertama sampai kelima masih gagal, solusi keenam adalah dengan menambahkan kode berikut di file “.htaccess”.
<IfModule mod_security.c>
SecFilterEngine Off
SecFilterScanPOST Off
</IfModule>

atau

<FilesMatch "(async-upload\.php|wp-cron\.php|xmlrpc\.php)$">
Satisfy Any
Order allow,deny
Allow from all
Deny from none
</FilesMatch>

Solusi Ketujuh:
Jika cara pertama sampai keenam masih gagal, kontak support web hosting tempat website Anda berada, karena kemungkinan PHP Memory Limit belum di set sesuai kebutuhan wordpress/plugins/theme yang terpasang di website Anda.

Semoga artikel ini bermanfaat.
diolah dari berbagai sumber dan pengalaman pribadi sebagai Hosting Provider.

by Khudri.
Supported by OIRY.NET

Implementation of Elgamal Elliptic Curve Cryptography Using Malab

IMPORTANT. This is not a full paragraph of this papers. Please download full papers. You can download from the URL below the end of this paragraph.

The idea of using elliptic curve in cryptography was introduced by Victor Miller [10] and Neal Koblitz as an alternative to established public key systems such as DSA and RSA. In 1985, they proposed a public key cryptosystems analogue of the ElGamal encryption schemes which used Elliptic Curve Discrete Logarithm Problem (ECDLP) [5,6,11]. According to Purbo and Wahyudi [11], Elliptic Curve Cryptography (ECC) can be used in some necessities such as encryption scheme (ElGamal ECC/EC ElGamal), digital signature (ECDSA) and key exchange protocol (Diffie Hellman
ECC/EC Diffie Hellman).

The most time consuming part of the computation is elliptic scalar multiplication. So we need to represent the multiplication algorithm ( see [5] and [6] ) to make the computation more efficient, such as binary algorithm, addition-subtraction algorithm and repeated-dobling algorithm. We use the addition-subtraction algorithm in our implementation and Non Adjacent Form (NAF) to represent the scalar. For computing the elliptic scalar multiplication k.P, k is represented by NAF form.

There are 3 main programmes which will be described in our implementation, they are:
1. Key Generation Programme.
2. Encryption Programme
3. Decryption Programme.
There are many functions must be made
to build the main programmes which
are classified into 3 categories, they are
1) Functon of Modular Arithmetics
2) Function of Elliptic Curve
Arithmatics
3) Function of ElGamal ECC.

International Conference (ICICI 2005)
“Implementation of ElGamal Elliptic Curve Cryptography Using Matlab “.
Download: Abstract | Full Papers | Source Code for Matlab Ver 7.

My Project (Essay, papers, Source Code, etc): https://wan.khudri.com
Tutorial, Article (All Download List): https://download.khudri.com

Abstract – Implementation of Elgamal Elliptic Curve Cryptography Using Malab

Author: Wan Khudri and Sutanto

ABSTRACT

ElGamal Elliptic Curve Cryptography(ECC) is a public key cryptography analogue of the ElGamal encryption schemes which is used Elliptic Curve Discrete Logarithm Problem (ECDLP). The software which is used to implement ElGamal ECC is MATLAB. This implementation consist of 3 main programmes, they are Key Generation, Encryption and Decryption ElGamal ECC. To reach the goal of the implementation, some functions which are able to construct the 3 main programmes are needed. Some functions are available in MATLAB and 31 functions are made by the writer himself. Those functions are classified into 3 categories, they are modular arithmetic function (7 functions), elliptic curve arithmetic function (5 functions) and ElGamal ECC function (19 functions).

The modular artihmetic function is used in addition operation, representation of NAF (Non Adjacent Form), multiplication operation, invers, division, power, and square root in modular arithmetic operation.

The elliptic curve arithmetic function is used in addition operation, elliptic curve equation, invers under addition, subtraction, and elliptic curve scalar multiplication.

The ElGamal function is used in biner-decimal conversion, decimal-biner conversion in ‘n’ bit format, to find lower and upper bound of key length, to generate prime number, to generate coefficient of elliptic curve equation, to find the order of the elliptic group, to generate one elliptic curve point, to calculate the order of point, to generate base point and its order, elliptic curve domain pa rameters, to generate private key and public key, to represent plaintext into number, number into point, point into number, number into plaintext, encryption of ElGamal ECC for one point, and decryption of ElGamal ECC for one chipertext of point.

Key Words: ElGamal, elliptic curve, cryptography, field, public key

International Conference (ICICI 2005)
“Implementation of ElGamal Elliptic Curve Cryptography Using Matlab “.
Download: Abstract | Full Papers | Source Code for Matlab Ver 7

My Project (Essay, papers, Source Code, etc): https://wan.khudri.com
Tutorial, Article (All Download List): https://download.khudri.com

Kriptografi Kurva Elliptic

Tahun 1985, Koblitz dan Miller mengenalkan kriptografi kurva elliptic (elliptic curve cryptography) yang menggunakan masalah logaritma diskrit pada titik kurva elliptic. Kriptografi kurva elliptic dapat digunakan untuk beberapa keperluan seperti skema enkripsi (contohnya ElGamal ECC), tanda tangan digital (contohnya ECDSA) dan protokol pertukaran kunci (contohnya Diffie-Hielman ECC).

Stallings [13] mendefinisikan kurva elliptic sebagai suatu kurva yang dibentuk oleh persamaan kubik dan memiliki persamaan umum

dengan A,B,C,D dan E adalah konstanta bilangan real. Domain x dan y adalah bilangan real (). Dalam penulisan ini, tidak dibahas mengenai persamaan (4.1). Untuk mendukung tujuan penulisan ini, penulis akan menjelaskan bentuk kurva yang lebih sederhana dari persamaan (4.1), yaitu

dengan A dan B dalam serta x, y .

Gambar 4.1 merupakan salah satu contoh bentuk geometri dari kurva elliptic dengan persamaan . Setiap kurva elliptic akan berbentuk simetris terhadap sumbu x atau garis y=0. Karena untuk setiap nilai x , terdapat sepasang nilai y yang memenuhi persamaan (4.2), yaitu

dan .

Kurva elliptic juga dapat dipandang sebagai suatu himpunan yang terdiri dari titik-titik (x,y) yang memenuhi persamaan (4.2). Himpunan tersebut dinotasikan dengan E(A,B). Untuk setiap nilai A dan B yang berbeda, dihasilkan himpunan E(A,B) yang berbeda pula. Sebagai contoh, kurva dalam Gambar 4.1 dan Gambar 4.2.

gbr-4-1
Gambar 4.1. Kurva Elliptic

gbr-4-2
Gambar 4.2. Kurva Elliptic

Source:
wan.khudri.com

Jenis-Jenis Kriptografi

Berdasarkan jenis kuncinya, algoritma kriptografi dapat dibagi menjadi dua kelompok yaitu algoritma simetri (konvensional / private key algorithm) dan algoritma asimetri (public key algorithm). Menurut Kurniawan [9], algoritma simetri adalah algoritma yang menggunakan kunci enkripsi yang sama dengan kunci dekripsinya. Pada algoritma ini, pengirim dan penerima harus menyetujui suatu kunci tertentu yang dinamakan kunci rahasia (secret key). Contohnya adalah DES (Data Encryption Standard), Rijndael, Blowfish dan lain-lain. Sedangkan algoritma asimetri didesain sedemikian sehingga kunci yang digunakan untuk enkripsi berbeda dengan kunci untuk dekripsi. Kunci yang digunakan untuk enkripsi disebut kunci publik (public key) dan dapat diketahui oleh orang lain. Sedangkan kunci untuk dekripsi dinamakan kunci rahasia atau sering disebut sebagai private key dan hanya diketahui oleh pemiliknya. Contohnya adalah ElGamal, RSA (Rivest-Shamir-Adleman), ECC (Elliptic Curve Cryptography) dan lain-lain.

Istilah “kunci rahasia” pada algoritma simetri digunakan untuk menyatakan kunci enkripsi sekaligus kunci dekripsi dan disebut secret key. Sedangkan pada algoritma asimetri, kunci rahasia hanya digunakan untuk menyatakan kunci dekripsi dan sering disebut sebagai private key. Hal ini dapat mengakibatkan kesalahan penafsiran pada istilah “kunci rahasia”. Karena itu, untuk pernyataan-pernyataan berikutnya digunakan istilah aslinya.

Menurut Purbo dan Wahyudi [11], saat ini terdapat tiga macam public key algorithm yang aman dan efisien berdasarkan permasalahan matematis, yaitu Integer Factorization Problem (IFP), Discrete Logarithm Problem (DLP) dan Elliptic Curve Discrete Logarithm Problem(ECDLP).

Jika diberikan bilangan bulat n yang merupakan hasil kali dua buah bilangan prima p dan q sehingga n=p.q, maka permasalahan matematis dalam IFP adalah mencari faktor dari n , yaitu p dan q. Contohnya adalah RSA.

DLP merupakan masalah yang didefinisikan pada aritmetika modular. Misalkan dipilih bilangan prima p dan diberikan bilangan bulat g (0<g<p-1) serta y merupakan pemangkatan dari g, sehingga . Permasalahan matematis dalam DLP adalah mencari x, jika diberikan pasangan bilangan g dan y. Contohnya adalah ElGamal, Diffie-Hellman, DSA (Disgital Signature Algorithm).

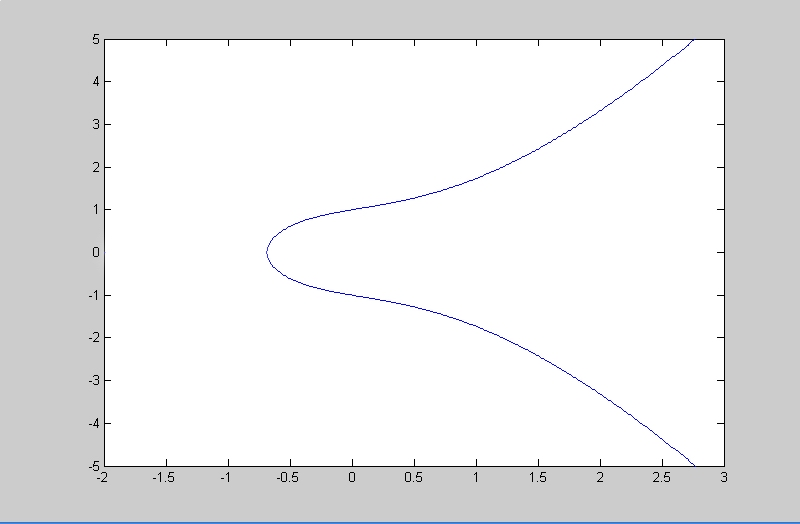
Jika Fp himpunan lapangan berhingga ( finite field ) , p bilangan prima,

P(xP,yP) titik pada kurva elliptik, dipilih V secara random sehingga Q=V.P. Permasalahan matematis dalam ECDLP adalah mencari V, jika diketahui titik P dan Q. Contohnya adalah ElGamal ECC (ElGamal Elliptic Curve Cryptography), ECDSA (Elliptic Curve Digital Signature Algorithm).

Algoritma ECC menggunakan ECDLP dan dikenalkan pertama kali oleh Koblitz dan Miller pada tahun 1985. ECC dapat digunakan untuk beberapa keperluan seperti skema enkripsi (contohnya ElGamal ECC), tanda tangan digital (contohnya ECDSA) dan protokol pertukaran kunci (contohnya Diffie Hellman ECC). Salah satu hal yang menarik mengenai ECC terletak pada tingkat keamanannya. ECC dapat menggunakan ukuran kunci yang lebih kecil dibandingkan dengan kriptografi lainnya dan memiliki tingkat keamanan yang sama. Kemampuan ini membuat ECC mempunyai keamanan yang terkuat dengan panjang kunci terpendek. Sebagai perbandingan, 160 bit ECC mempunyai tingkat keamanan yang sama dengan 1024 bit RSA atau DSA dan 224 bit ECC memiliki tingkat keamanan yang sama dengan 2048 bit RSA atau DSA [6,9,11].

Kemampuan dan keamanan ECC ini yang membuat penulis tertarik untuk mengkaji lebih dalam tentang salah satu skema enkripsinya, yaitu ElGamal ECC (ElGamal Elliptic Curve Cryptography) dan membuat program aplikasinya.

Source:
wan.khudri.com

Kriptografi ?

Teknologi informasi semakin berkembang. Perkembangan tersebut secara langsung maupun tidak langsung mempengaruhi sistem perdagangan, transaksi dan sistem informasi selama ini. Terutama di era internet ini, semua informasi terkirim dengan bebas melalui suatu jaringan dengan tingkat keamanan yang relatif rendah. Untuk itulah peranan teknologi keamanan informasi benar-benar dibutuhkan. Keamanan informasi (information security) merupakan bagian yang sangat penting dari sebuah sistem dalam jaringan komputer terutama yang terhubung dengan internet. Sebuah sistem yang mempermudah dan memanjakan pengguna tidak akan berguna tanpa didukung oleh sistem keamanan yang tinggi. Oleh karena itu, informasi atau data rahasia yang akan dikirim harus disandikan agar tidak dapat dibaca oleh orang lain.

Teknik untuk mengubah informasi yang dapat dibaca/teks asli (plaintext) menjadi kode-kode tertentu disebut sebagai enkripsi (encryption) dan hasilnya disebut chipertext. Sedangkan teknik untuk mengubah chipertext menjadi plaintext disebut dekripsi (decryption). Algoritma yang digunakan untuk proses enkripsi dan dekripsi adalah algoritma kriptografi (cryptographic algorithm) atau sering disebut chiper. Algoritma kriptografi ini bekerja dengan menggunakan kunci (key) seperti kata, nomor maupun frase tetentu. Jika dilakukan enkripsi pada plaintext yang sama dengan menggunakan kunci yang berbeda, maka akan menjadi chipertext yang berbeda [11].

Menurut Menezes et al. [10], Doraiswamy et al. [6] dan Kurniawan [9], kriptografi (cryptography) adalah seni dan ilmu pengetahuan untuk menjaga keamanan informasi. Orangnya disebut sebagai cryptographer. Kebalikan dari kriptografi adalah cryptanalysis, yaitu seni dan ilmu untuk memecahkan chipertext menjadi plaintext tanpa melalui cara yang seharusnya. Orangnya disebut sebagai cryptanalyst.

Source:
wan.khudri.com